Q1¶
Give numerical values to 3 decimal places (with units, if relevant) for the following physical and mathematical constants:
- $\pi$
- $e$
- $N_\text{A}$
- $R$
- $k_\text{B}$
- $c$
- $h$
- $\hbar$
Q2¶
Give an order of magnitude estimate for the following physical constants:
- $e_o$ (fundamental charge)
- $m_\text{P}$ (proton mass)
- Atomic Mass Unit
- $m_\text{e}$ (electron mass)
Q3¶
Complete the square: $$f(x) = a x^2 + b x + c ,$$ i.e., write this expression in the form $f(x) = \alpha \left( x + \beta \right)^2 + \gamma$ .
First divide through by $a$ so that the $x^2$ term has no coefficient:$$\frac{f(x)}{a} = x^2 + \frac{b}{a} + \frac{c}{a}$$Now add and subtract $\frac{b^2}{4 a^2}$ (i.e., the square of one-half the second term):$$\frac{f(x)}{a} = \left( x^2 + \frac{b}{a} + \frac{b^2}{4a^2} \right) - \frac{b^2}{4a^2} + \frac{c}{a}$$The term in parentheses can now be rewritten as a square$$\frac{f(x)}{a} = \left( x + \frac{b}{2a} \right)^2 - \frac{b^2}{4a^2} + \frac{c}{a}$$so that $$f(x) = a \left( x + \frac{b}{2a} \right)^2 + \left( c - \frac{b^2}{4a} \right) .$$Thus the problem is solved with \begin{align*} \alpha &= a\\ \beta &= \frac{b}{2a} \\ \gamma &= c - \frac{b^2}{4a} .\end{align*}
Q4¶
Calculate the eigenvalues of the matrix$$\begin{bmatrix} -\frac{\Delta}{2} & V \\ V & \frac{\Delta}{2} .\end{bmatrix} $$
The eigenvalues are the roots of the determinant $$ 0 = \left | \begin{matrix} -\frac{\Delta}{2} -\lambda & V \\ V & \frac{\Delta}{2} -\lambda \end{matrix} \right | = \lambda^2 - \frac{\Delta^2}{4} - V^2 ,$$which are obtained from the quadratic formula as $$\lambda_{\pm} = \pm \frac{1}{2} \sqrt{\Delta^2 + 4V^2} . $$
Q5¶
Calculate (assuming you know the eigenvalues) the eigenvectors of the matrix$$\begin{bmatrix} -\frac{\Delta}{2} & V \\ V & \frac{\Delta}{2} .\end{bmatrix} $$
Eigenvectors are defined by the criterion that$$\begin{bmatrix} -\frac{\Delta}{2} -\lambda_\pm & V \\ V & \frac{\Delta}{2} -\lambda_\pm \end{bmatrix} \begin{bmatrix} u_1^{(\pm)} \\ u_2^{(\pm)} \end{bmatrix} = 0 .$$This matrix equation is really two separate equations, one obtained from the top row and one from the bottom row of the matrix. Only one of these is needed to calculate eigenvector coefficients. Using only the top row, we get the condition$$- \left( \frac{\Delta}{2} + \lambda_{\pm} \right) u_1^{(\pm)} + V u_2^{(\pm)} = 0$$or$$u_2^{(\pm)} = \frac{\lambda_{\pm} + \frac{\Delta}{2}}{V} u_1^{(\pm)} . $$If we define$$\phi_{\pm} = \text{atan} \left( \frac{\lambda_{\pm} + \frac{\Delta}{2}}{V} \right) $$then since$$ \sin \phi_{\pm} = \tan \phi_{\pm} \cos \phi_\pm,$$the eigenvalue condition is satisfied by setting$$ u_{1}^{(\pm)} = \cos \phi_{\pm}$$$$ u_{2}^{(\pm)} = \sin \phi_{\pm}.$$
Q6¶
Evaluate the following derivatives:
- $\frac{d}{dx} x^n$
- $\frac{d}{dx} \ln x$
- $\frac{d}{dx} e^{ax}$
- $\frac{d}{dx} \cos \left( a x \right)$
- $\frac{d}{dx} \sin \left( a x \right) $
Q7¶
Evaluate the integral$$\int_0^\infty dt \; e^{-\gamma t}$$
Since $\frac{d e^{-\gamma t}}{dt} = - \gamma e^{-\gamma t}$, $$\int_0^\infty dt \; e^{-\gamma t} = -\left .\frac{e^{-\gamma t}}{\gamma} \right|_{0}^\infty = \frac{1}{\gamma}.$$
Q8¶
Evaluate the integral$$\int_0^\infty dt \; e^{-\gamma t} t^n .$$
This is a perfect case to use integration by parts. First, we write the integral in the form $\int u dv$ by defining$$ u = t^n \leftrightarrow du = n t^{n-1} dt$$$$ dv = e^{-\gamma t} dt \leftrightarrow v = -\frac{e^{-\gamma t}}{\gamma} . $$Then using the integration-by-parts formula$$ \int u dv = uv - \int v du,$$we get$$\int_0^\infty dt \; e^{-\gamma t} t^n = - \left . \frac{t^n e^{-\gamma t}}{\gamma} \right|_0^\infty + \frac{n}{\gamma} \int_0^\infty dt \; e^{-\gamma t} t^{n-1} .$$The first of these terms vanishes, while the second is just $\frac{n}{\gamma}$ times the original integral with $n$ replaced with $n-1$. Repeating this process $n-1$ times, we obtain$$\int_0^\infty dt \; e^{-\gamma t} t^n = \frac{n\cdot (n-1)\cdot ... \cdot 3\cdot 2}{\gamma^{n-1}} \int_0^\infty dt \; e^{-\gamma t} t^0 = \frac{n!}{\gamma^n}.$$When $n$ is not an integer, and $\gamma = 1$, this integral defines the Gamma function. (But note that $\Gamma(x)$ is defined so that $\Gamma(n) = (n-1)!$.)
Q9¶
Evaluate the integral$$\int_{0}^\infty dt \; e^{i \omega t} e^{-\gamma t}$$
\begin{align} \int_{0}^\infty dt \; e^{i \omega t} e^{-\gamma t} = \int_{0}^\infty dt \; e^{ \left( i \omega - \gamma \right) t} = \frac{1}{i \omega - \gamma}\end{align}
Q10¶
Evaluate the integral$$\int_{-\infty}^\infty dt \; e^{i \omega t} e^{-\gamma |t|}$$
Splitting up the integral as \begin{align} \int_{-\infty}^\infty dt \; e^{i \omega t} e^{-\gamma |t|} &= \int_{-\infty}^0 dt \; e^{i \omega t} e^{+\gamma t} + \int_{0}^\infty dt \; e^{i \omega t} e^{-\gamma t} \nonumber \\ &= \int_{0}^\infty dt \; e^{-i \omega t} e^{-\gamma t} + \int_{0}^\infty dt \; e^{i \omega t} e^{-\gamma t}\end{align}casts this as a sum of two integrals with the same form as in the last question. Thus$$\int_{-\infty}^\infty dt \; e^{i \omega t} e^{-\gamma |t|} = \frac{1}{-i\omega + \gamma} + \frac{1}{i \omega + \gamma } = \frac{2 \gamma}{\omega^2 + \gamma^2 } . $$
Q11¶
Evaluate the integral$$\int_{-\infty}^\infty e^{-\frac{(x-x_o)^2}{2\sigma^2}} dx $$
As a first step: memorize the solution! (A good PChemist will need to evaluate integrals like this quite often.) The answer is$$\int_{-\infty}^\infty e^{-\frac{(x-x_o)^2}{2\sigma^2}} dx = \sqrt{2 \pi \sigma^2} .$$To actually calculate the integral, first make the replacement $u = \frac{x - x_o}{\sqrt{2 \sigma^2}}$ so that $$\int_{-\infty}^\infty e^{-\frac{(x-x_o)^2}{2\sigma^2}} dx = \sqrt{2 \sigma^2} \int_{-\infty}^\infty e^{-u^2} du.$$Evaluating the integral $du$ is (somewhat counterintuitively) much easier in two dimensions. Note that $$ \int_{-\infty}^\infty e^{-u^2} du = \left [ \int_{-\infty}^\infty e^{-u^2} du \int_{-\infty}^\infty e^{-v^2} dv\right]^\frac{1}{2}, $$since the double integral is simply the single integral squared. But the double-integral is easy to evaluate in polar coordinates:$$ \int_{-\infty}^\infty e^{-u^2} du \int_{-\infty}^\infty e^{-v^2} dv = \int_0^{2\pi} d\theta \int_0^\infty dr \;r e^{-r^2} = 2 \pi \left .\left( - \frac{e^{-r^2}}{2} \right) \right|_0^\infty = \pi.$$The additional factor of $r$ here (the reason we can directly evaluate the integral) comes from the fact that (for infinitesimal displacements) in two dimensions $ dx dy = r dr d\theta $. Finally, this allows us to write the original integral as $$ \int_{-\infty}^\infty e^{-\frac{(x-x_o)^2}{2\sigma^2}} dx = \sqrt{2 \sigma^2} \left [ \int_{-\infty}^\infty e^{-u^2} du \int_{-\infty}^\infty e^{-v^2} dv\right]^\frac{1}{2} = \sqrt{2 \pi \sigma^2 } .$$
Q12¶
Calculate the Fourier transform$$\int_{-\infty}^\infty e^{i \omega t} e^{-\frac{(t-t_o)^2}{2 \sigma^2}} dt $$
First introduce the change of variables $$ u = \frac{t - t_o}{\sqrt{2 \sigma}} \leftrightarrow \sqrt{2} \sigma u + t_o = t$$to obtain\begin{align} \int_{-\infty}^\infty e^{i \omega t} e^{-\frac{(t-t_o)^2}{2 \sigma^2}} dt &= \int_{-\infty}^\infty e^{i \omega \left( \sqrt{2} \sigma u + t_o\right)} e^{-u^2} \left(\sqrt{2} \sigma du\right) \nonumber \\ &= \sqrt{2} \sigma e^{i \omega t_o} \int_{-\infty}^\infty e^{-u^2 + i \omega \sqrt{2} \sigma u} du .\end{align}Now complete the square:\begin{align} \int_{-\infty}^\infty e^{i \omega t} e^{-\frac{(t-t_o)^2}{2 \sigma^2}} dt &= \sqrt{2} \sigma e^{i \omega t_o} \int_{-\infty}^\infty e^{- \left( u^2 - i \omega \sqrt{2} \sigma u - \frac{\omega^2 \sigma^2}{2} \right) - \frac{\omega^2 \sigma^2 }{2} } du \nonumber \\ &= \sqrt{2}\sigma e^{i \omega t_o} e^{- \frac{\omega^2 \sigma^2}{2} } \int_{-\infty}^\infty e^{- \left( u - i \frac{\omega \sigma}{\sqrt{2}} \right)^2} du\\ &= \sqrt{2} \sigma e^{i \omega t_o} e^{- \frac{\omega^2\sigma^2}{2} } \int_{-\infty}^\infty e^{- u^2} du,\end{align}where in the last line, we have noted that the shift term $i \frac{\sigma \omega}{\sqrt{2}}$ doesn't affect the overall value of the integral. Using the Gaussian integral identity in the last question, we finally obtain $$ \int_{-\infty}^\infty e^{i \omega t} e^{-\frac{(t-t_o)^2}{2 \sigma^2}} dt = \sqrt{2\pi \sigma^2} e^{i \omega t_o} e^{- \frac{\sigma^2 \omega^2}{2} } .$$
Q13¶
Complete the summation $$\sum_{n} \frac{x^n}{n!}$$
$$\sum_{n} \frac{x^n}{n!} = e^{x} .$$This can be established as a Taylor series for $e^x$:$$e^x = 1 + \left .\frac{d e^x}{dx} \right |_{x=0} x + \left .\frac{d^2 e^x}{dx^2} \right |_{x=0} \frac{x^2}{2!} + \left .\frac{d^3 e^x}{dx^3} \right |_{x=0} \frac{x^3}{3!} + ... . $$
Q14¶
Complete the summation $$\sum_n x^n $$
$$ \sum_n x^n = \frac{1}{1-x} .$$This can be established either as a Taylor series or by recognizing that for any $n > 0$:\begin{align} \left( 1 - x \right) \left( 1 + x + x^2 + x^3 + ... + x^n \right) = 1 - x^{n+1} . \end{align}Rearranging this equation gives\begin{align} 1 + x + x^2 + x^3 + ... + x^n = \frac{1 - x^{n+1}}{1 - x} ,\end{align}which converges as $n \to \infty$ to$$ \frac{1}{1 - x} = 1 + x + x^2 + ... .$$
Q15¶
Give the Taylor series to first non-vanishing order around $x=0$:
- $e^x $
- $\sqrt{1+x} $
- $\frac{1}{1-x}$
- $\sin(x)$
- $\cos(x)$
Q16¶
Express $e^{i\theta}$ in terms of $\sin$ and $\cos$ contributions.
$e^{i\theta} = \cos \theta + i \sin \theta$
Q17¶
Express $\sin \theta $ and $\cos \theta$ in terms of $e^{i\theta}$ and $e^{-i\theta}$ contributions.
Adding the Euler identities for $\sin \theta$ and $\sin (-\theta) = - \sin \theta$ gives:$$\sin \theta = \frac{e^{i\theta} - e^{-i \theta}}{2i}.$$Adding the Euler identities for $\cos \theta$ and $\cos (-\theta) = \cos \theta$ gives:$$\cos \theta = \frac{e^{i\theta} + e^{-i \theta}}{2}.$$
Q18¶
Express $\cos \theta \cos \phi$ in terms of $\cos \left( \theta + \phi \right)$ and $\cos \left( \theta - \phi \right)$.
Using the Euler identity to express $\cos \left( \theta + \phi \right)$, we have$$4 \cos \theta \cos \phi = \left( e^{i \theta} + e^{-i \theta} \right) \left( e^{i \phi} + e^{-i \phi} \right) = e^{i \left( \theta + \phi \right)} + e^{-i \left( \theta + \phi \right)} + e^{i \left( \theta - \phi \right)} + e^{-i \left( \theta - \phi \right)} .$$Regrouping terms and dividing through by 4 gives$$ \cos \theta \cos \phi = \frac{1}{2} \left [ \cos \left( \theta + \phi \right) + \cos \left( \theta - \phi \right) \right].$$
Q19¶
Express $\sin \theta \sin \phi$ in terms of $\cos \left( \theta + \phi \right)$ and $\cos \left( \theta - \phi \right)$.
Using the Euler identity to express $\sin \left( \theta + \phi \right)$, we have$$ \left( 2i \right)^2 \sin \theta \sin \phi = \left( e^{i \theta} - e^{-i \theta} \right) \left( e^{i \phi} - e^{-i \phi} \right) = e^{i \left( \theta + \phi \right)} + e^{-i \left( \theta + \phi \right)} - e^{i \left( \theta - \phi \right)} - e^{-i \left( \theta - \phi \right)} .$$Regrouping terms and dividing through by 4 gives$$ \sin \theta \sin \phi = \frac{1}{2} \left [ \cos \left( \theta - \phi \right) - \cos \left( \theta + \phi \right) \right].$$
Q20¶
Express $\sin \theta \cos \phi$ in terms of $\sin \left( \theta + \phi \right) $ and $\sin \left( \theta - \phi \right)$.
Expanding using the Euler identity gives$$ 4 i \sin \theta \cos \phi = \left( e^{i \theta} - e^{-i \theta} \right) \left( e^{i \phi} + e^{-i \phi} \right) = e^{i (\theta + \phi) } - e^{-i (\theta + \phi)} + e^{i (\theta - \phi)} - e^{-i (\theta - \phi)} . $$Regrouping terms and dividing by $4i$ gives$$ \sin \theta \cos \phi = \frac{1}{2} \left [ \sin \left( \theta + \phi \right) + \sin \left( \theta - \phi \right) \right] . $$
Q21¶
Express $\cos\left( \theta + \phi \right) $ and $\sin\left( \theta + \phi \right) $ in terms of $\cos \theta, \cos \phi$, $\sin \theta$, and $\sin \phi$.
From the previous three identities, we have:\begin{align*} 2 \cos \theta \cos \phi &= \cos \left( \theta + \phi \right) + \cos \left( \theta - \phi \right)\\ 2\sin \theta \sin \phi &= \cos \left( \theta - \phi \right) - \cos \left( \theta + \phi \right) \\ 2 \sin \theta \cos \phi &= \sin \left( \theta + \phi \right) + \sin \left( \theta - \phi \right) \\ 2 \cos \theta \sin \phi &= \sin \left( \theta + \phi \right) - \sin \left( \theta - \phi \right) .\end{align*}The difference of the first two equations produces$$\cos\left( \theta + \phi \right) = \cos \theta \cos \phi - \sin \theta \sin \phi .$$The sum of the last two equations produces$$ \sin \left( \theta + \phi \right) = \sin \theta \cos \phi + \cos \theta \sin \phi .$$
Algebra
Q22¶
What are the defining properties of a mathematical group?
A group is a set of elements $a, b, c, ...$ together with an operation $\circ$ that satisfies the following properties:
Q23¶
What is a symmetry operation?
A symmetry operation is a geometric transformation (e.g., rotation or inversion) that leaves a system unchanged from its starting configuration.
Q24¶
What is a point group?
A point group is a group of symmetry operations that share a fixed point.
Q25¶
What are the four basic classes of molecular symmetry operations (other than the identity)?
Q26¶
Give examples of both proper and improper rotations in methane.
The axes that bisect each pair of H atoms in methane (CH$_4$) are both proper and improper rotation axes. If the molecule is rotated by 180$^\text{o}$ around one of these axes, it is brought back to its original configuration (a proper rotation). If it is rotated by 90$^\text{o}$ around the axis and then reflected through the plane orthogonal to it, it is likewise brought back to the original configuration (an improper rotation).
Q27¶
The figure below illustrates the rotation of a point $(x_0,y_0)$ through an angle $\phi$ in the $(x,y)$ plane. Give an expression for $x_1$ and $y_1$ in terms of the initial coordinates $(x_0, y_0)$ and the angles $\theta$ and $\phi$.\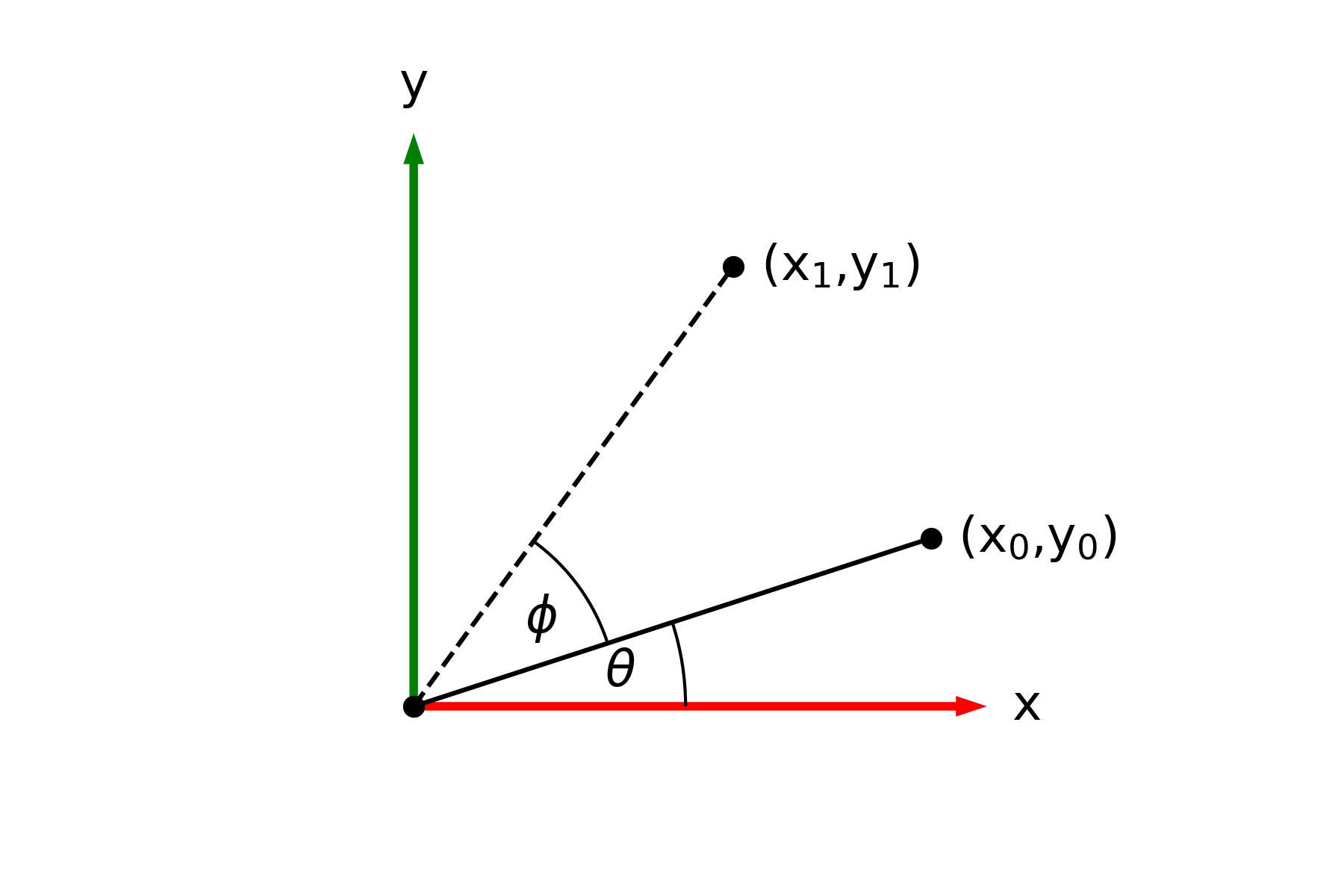
If we let $L = \sqrt{x_0^2 + y_0^2} = \sqrt{x_1^2 + y_1^2}$, then by definition of the $\sin$ and $\cos$ functions, \begin{align*} x_0 &= L \cos \theta \\ y_0 &= L \sin \theta \\ x_1 &= L \cos\left( \theta + \phi \right) \\ y_1 &= L \sin \left( \theta + \phi \right) .\end{align*}Using the angle-sum identities stated earlier, these can be expanded as\begin{align*} x_1 &= L \cos\left( \theta + \phi \right) \\ &= L \cos \theta \cos \phi - L \sin \theta \sin \phi \\ &= \left( \cos \phi \right ) x_0 - \left( \sin \phi \right) y_0 .\end{align*}and \begin{align*} y_1 &= L \sin \left( \theta + \phi \right) \\ &= L \sin \theta \cos \phi + L \cos \theta \sin \phi \\ &= \left( \sin \phi \right ) x_0 + \left( \cos \phi \right) y_0 .\end{align*}
Q28¶
Give the 3x3 rotation matrix that corresponds to rotation around the $z$ axis by an angle $\phi$.
Rotation around the $z$ axis corresponds to rotating all $(x,y)$ coordinates in the $xy$ plane and leaving all $z$ coordinates unchanged. According to the last problem, the points thus transform as \begin{align*} x &\to \left( \cos \phi \right) x_0 - \left( \sin \phi \right) y_0 \\ y &\to \left( \sin \phi \right) x_0 + \left( \cos \phi \right) y_0 \\ z &\to z .\end{align*}In matrix form, the new coordinates $(x',y',z')$ are given by$$ \begin{bmatrix} x'\\y'\\z' \end{bmatrix} = \begin{bmatrix} \cos \phi & -\sin \phi & 0 \\ \sin \phi & \cos \phi & 0 \\ 0 & 0 & 1\end{bmatrix} \begin{bmatrix} x\\y\\z\end{bmatrix} . $$Thus the desired rotation matrix is $${\boldsymbol R}_z(\phi) = \begin{bmatrix} \cos \phi & -\sin \phi & 0 \\ \sin \phi & \cos \phi & 0 \\ 0 & 0 & 1\end{bmatrix} .$$
Quantum Mechanics
Q29¶
What is the time-dependent Schrodinger equation?
$$ i \hbar \frac{\partial \psi}{\partial t} = \hat H \psi, $$where $\psi$ is the wavefunction (or wavevector), and $\hat H$ is the Hamiltonian operator, corresponding to the total system energy.
Q30¶
What is the time-independent Schrodinger equation?
Q31¶
Why does the time-dependent Schrodinger equation naturally lead to the time-independent Schrodinger equation?
Q32¶
Express the operators $\hat x$ and $\hat p$ in the position basis.
Q33¶
Express the operators $\hat x$ and $\hat p$ in the momentum basis.
Q34¶
Demonstrate the canonical commutation relation from the position-basis representation of $\hat x$ and $\hat p$.
Q35¶
What is the general form in the position basis for the quantum Hamiltonian of a particle of mass $M$ in a one-dimensional potential $V(x)$?
Q36¶
Find the eigenfunctions and eigenvalues of the potential $$V(x) = \left \{ \begin{matrix} 0, & -\frac{L}{2} \leq x \leq \frac{L}{2} \\\infty, & \text{otherwise.} \end{matrix} \right. $$
\question{Find the eigenfunctions and eigenvalues of the potential $$V(x) = \left \{ \begin{matrix} 0, & -\frac{L}{2} \leq x \leq \frac{L}{2} \\\infty, & \text{otherwise.} \end{matrix} \right. $$}
Q37¶
Write the harmonic oscillator Hamiltonian (with potential $V(x) = \frac{m \omega^2 x^2}{2}$) in terms of
- $\hat x$ and $\hat p$ operators in the position basis,
- mass-weighted $\hat Q$ and $\hat P$ operators, and
- raising and lowering operators $\hat a$ and $\hat a^\dagger$ .
Q38¶
Calculate the commutator $\left [ \hat a , a^\dagger \right]$.
Q39¶
Calculate the commutator $\left [ \hat H , a^\dagger \right]$
Q40¶
Calculate the commutator $\left [ \hat H , a \right]$
Q41¶
Show that if $\phi$ is an eigenfunction of the harmonic Hamiltonian $\hat H$ with eigenvalue $\lambda$ then $\hat a \phi$ is an eigenfunction of $\hat H$ with eigenvalue $\lambda - \hbar \omega$.
Q42¶
Show that if $\phi$ is an eigenfunction of the harmonic Hamiltonian $\hat H$ with eigenvalue $\lambda$ then $\hat a^\dagger \phi$ is an eigenfunction of $\hat H$ with eigenvalue $\lambda + \hbar \omega$.
Q43¶
If $\phi$ is a normalized eigenfunction of the harmonic Hamiltonian $\hat H$, what is $\| \hat a \phi \|^2$?
Q44¶
If $\phi$ is a normalized eigenfunction of the harmonic Hamiltonian $\hat H$, what is $\| \hat a^\dagger \phi \|^2$?
Q45¶
Derive a lower bound on the eigenvalues of the harmonic oscillator Hamiltonian. What is the smallest eigenvalue $\lambda_o$ of $\hat H$? How do you know that this is a valid eigenvalue?
Q46¶
Use the position-basis representation of $\hat x$, $\hat p$, and $\hat a$ to find the ground-state eigenfunction $\phi_0$ of the harmonic oscillator.
Q47¶
Consider the two-dimensional harmonic oscillator potential $$V(x_1,x_2) = \frac{m \omega_1^2 x_1^2}{2} + v x_1 x_2 + \frac{m \omega_2^2 x_2^2}{2} .$$ What is the Hessian for this system? What are its normal-mode frequencies?
Q48¶
What does the ``ket'' $\left | \psi\right \rangle$ represent in wave mechanics? What about in matrix mechanics?
Q49¶
What does the ``bra'' $\left \langle \psi\right |$ represent in wave mechanics? What about in matrix mechanics?
Q50¶
How is the adjoint of an operator defined?
Q51¶
How is a Hermitian operator defined?
Q52¶
Prove that the eigenvalues of a Hermitian operator are real.
Q53¶
Prove that non-degenerate eigenvectors of a Hermitian operator are orthogonal.
Q54¶
Derive the variational principle, i.e., show that for any Hermitian operator $\hat A$ with a lower bound $\lambda_o$ on its eigenvalues, $$ \left \langle \psi \left |\hat A \right |\psi\right \rangle \geq \lambda_o.$$
Q55¶
Derive the quantum Adiabatic Theorem.
Q56¶
What (Schrodinger-like) equation defines the time-evolution operator $\hat U(t,t_o)$?
Q57¶
What form does $\hat U(t,t_o)$ take under a static (time-indepdendent) Hamiltonian?
Q58¶
Write down an expression for the density matrix of a system of $N$ independent particles, each with wavefunction $\left | \psi_n\right \rangle$.
Q59¶
How do you calculate the expectation value $\left \langle A \right \rangle $ for an operator $\hat A$ from the density matrix $\hat \rho$?
Q60¶
Show that the trace of an operator is independent of the basis used to evaluate it.
Q61¶
What is the quantum Liouville equation?
Q62¶
Derive the quantum Liouville equation from the time-dependent Schrodinger equation.
Q63¶
Show that the trace is invariant under cyclic permutations.
Q64¶
Consider a system with Hamiltonian $\hat H = \hat H_\text{o} + \hat V$, where $\hat V$ can be considered a small perturbation. How is the interaction-picture density matrix $\hat \rho_\text{I}$ defined for this system?
Q65¶
Consider a system with Hamiltonian $\hat H = \hat H_\text{o} + \hat V$, where $\hat V$ can be considered a small perturbation. What is the Liouville equation for the interaction-picture density matrix $\hat \rho_\text{I}$ for this system?
Q66¶
Consider a system with Hamiltonian $\hat H = \hat H_\text{o} + \hat V$, where $\hat V$ can be considered a small perturbation. Derive the Dyson series expansion for $\hat \rho_\text{I}(t)$ by formally integrating the Liouville equation for $\hat \rho_\text{I}$ and repeatedly plugging the answer into itself.
Thermodynamics and Statistical Mechanics
Q67¶
What is the First Law of Thermodynamics? (Include a statement of the law as an equation).
Q68¶
Write down the differential for $dW$ in a system with only PV work.
Q69¶
What is the thermodynamic definition of entropy?
Q70¶
Write down a differential statement of the First Law of thermodynamics for a system with only PV work.
Q71¶
What does the differential statement of the First Law tell you about the physical interpretation of $P$ and $T$?
Q72¶
What is the Second Law of Thermodynamics?
Q73¶
What does a heat capacity tell you? What is the difference between $C_\text{P}$ and $C_\text{V}$?
Q74¶
Give an expression for the energy of a monatomic ideal gas in terms of macroscopic parameters.
Q75¶
What is the equation of state for an ideal gas?
Q76¶
What do the following terms mean in the context of thermodynamics?
- Adiabatic
- Isothermal
- Isobaric
- Isochoric
Q77¶
What is $C_\text{V}$ for an ideal gas? What is $C_\text{P}$?
Q78¶
Under what circumstances is Entropy maximized at equilibrium? (Use the Second Law to prove this.)
Q79¶
How is enthalpy defined? What is its physical meaning?
Q80¶
Under what circumstances is the Enthalpy maximized at equilibrium? (Use the Second Law to prove this.)
Q81¶
What is the definition of the Gibbs Free Energy? What is its physical meaning?
Q82¶
Under what circumstances is the Gibbs Free Energy maximized at equilibrium? (Use the Second Law to prove this.)
Q83¶
What is the definition of the Helmholtz Free Energy? What is its physical meaning?
Q84¶
Under what circumstances is the Helmholtz Free Energy maximized at equilibrium? (Use the Second Law to prove this.)
Q85¶
What variables are held constant in each of the following?
- Microcanonical ensemble
- Canonical ensemble
- Gibbs ensemble
- Grand canonical ensemble
Q86¶
Give an equation for the information entropy $s\left( \{ p_\mu \} \right)$ of a discrete probability distribution $\{ p_\mu \}$. What does $s\left( \{ p_\mu \} \right)$ represent intuitively?
Q87¶
What is the relationship between information entropy and thermodynamic entropy?
Q88¶
How are microstate probabilities $p_\mu$ assigned in the microcanonical ensemble?
Q89¶
How are microstate probabilities $p_\mu$ assigned in the canonical ensemble?
Q90¶
How are microstate probabilities $p_\mu$ assigned in the Gibbs ensemble?
Q91¶
How are microstate probabilities $p_\mu$ assigned in the Grand canonical ensemble?
Spectroscopy
Q92¶
What is the field-dipole Hamiltonian for light-matter interactions?
Q93¶
Consider a system with a static Hamiltonian $\hat H_\text{o}$ perturbed by the field-dipole interaction with the electric field that is zero for $t \leq 0$. What is the first-order correction $\psi_\text{I}^{(1)}(t)$ to the interaction-picture representation of the wavefunction for $t > 0$?
Q94¶
Consider a system with a static Hamiltonian $\hat H_\text{o}$ perturbed by the field-dipole interaction with the electric field that is zero for $t \leq 0$. What is the first-order correction $\hat \rho_\text{I}^{(1)}(t)$ to the interaction-picture representation of the density matrix for $t > 0$?
Q95¶
Give an expression for the linear polarization $\vec P^{(1)}(t)$ of an isotropic material in terms of its linear response function $R^{(1)}(\tau)$.
Q96¶
Give an expression for the linear response tensor $R_{\alpha\beta}^{(1)}(\tau)$ as an autocorrelation function.
Q97¶
What is the relationship between the linear response function $R^{(1)}(\tau)$ for an isotropic material and the linear susceptibility $\chi^{(1)}(\omega)$
Q98¶
What is the relationship between the linear linear susceptibility $\chi^{(1)}(\omega)$ for an isotropic material and the permittivity $\varepsilon(\omega)$?
Q99¶
What is the relationship between the permittivity $\varepsilon(\omega)$ and the refractive index $n(\omega)$?
Q100¶
What is the relationship between the permittivity $\varepsilon(\omega)$ and the extinction coefficient $\kappa(\omega)$?
Q101¶
What is the (a) exact and (b) low-OD approximate relationship between $\kappa(\omega)$ and $\chi^{(1)}(\omega)$?
Q102¶
What is the difference between homogeneous and inhomogeneous broadening? What is meant by ``static disorder''?
Q103¶
What is the difference between dissipation and dephasing?
Q104¶
What is motional narrowing? What sets the timescale upon which motional narrowing occurs?
Q105¶
Roughly how many cm$^{-1}$ are there per nm in the vicinity of each of the following?
- 700 nm:
- 500 nm:
- 300 nm:
Q108¶
What is the oscillation period in vacuum of a
- 9 $\mu$m light wave?
- 6 $\mu$m light wave?
- 3 $\mu$m light wave?
- 900 nm light wave?
- 600 nm light wave?
- 300 nm light wave?
0